• Image

  
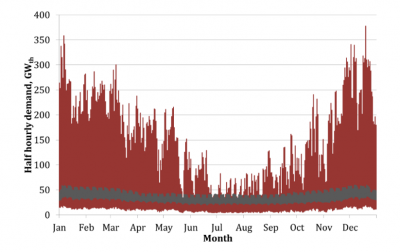
  The ground-breaking research of Robert Sansom at Imperial College London generated the first profile of half-hourly heat demand, reflected in the chart to the right that has become famous in energy-policy circles for illustrating the challenge of matching heat demand to inflexible sources:[1]
• Image

  
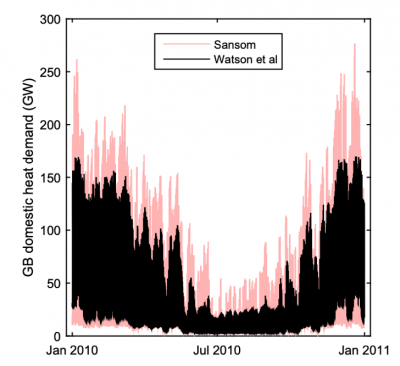
  Recently, Watson, Lomas and Buswell of Loughborough University made some well-founded modifications to Sansom’s model that reduced its “peakiness”.[2] The observation that heat demand would be spread more widely over the day in cold conditions with high demand (rather than simply increased pro rata in each period) is both intuitive and consistent with the large dataset that they used. The difference with Sansom is illustrated in the chart from their paper to the right.
   

  We adopted their “less-peaky” heat-demand profiles to convert National Grid’s daily gas-demand figures into reasonable synthetic hourly figures.[3] The somewhat-flattened profile reduces the balancing challenge, but comparing the two charts above should illustrate that heat demand remains significantly larger and more variable than electricity demand (the grey line in Sansom’s chart).

• The available solar figures do not reflect national output, and
• The embedded solar is treated as negative demand and affects Elexon’s demand figures

However, the profile of grid-connected solar output is probably reasonably reflective of the profile of total solar output (although the embedded solar is probably somewhat less optimally positioned on average). So we can use Elexon’s solar figures for the hourly solar profile whilst discarding the absolute figures as only a fraction of the true figure. In our model, we treat solar as one homogeneous lump of capacity (undifferentiated as grid-connected or embedded), and likewise electricity demand as a gross figure exclusive of any embedded power, to minimise complexity. That means that the model figures for electricity demand will not match the metered figures and the figures in national statistics. But reverse-engineering these figures (by applying the solar profile to an estimate of embedded capacity based on subtracting the public figures for total capacity from Elexon’s figures for grid-connected capacity) should be reasonably accurate, and produce the same net effect.

• If we were historically exporting strongly in a period but our model predicts under different conditions that we would have a high need to import in that period, we assume that the UK would not choose to export, but the neighbour would have its own requirements that prevented substantial export to us, and treat it as a wash.
• If historical flows were not large up or down in a period, and the model calculates that the UK needs to import or export heavily in that period under different conditions, we assume that the neighbour was not stressed and would be able to accommodate the UK’s requirements.
• If the model predicts that the UK will not be under significant stress in a period, but a neighbour (most often Ireland) was relying heavily on us historically in that period, the model assumes that we will continue to accommodate that.

• Nuclear is the key one. Although it can be varied, its economics mean that it rarely is. It does, however, occasionally experience step changes when one of the units has to shutdown for maintenance. Each unit is so large that these steps are material. We reflect this by using Elexon’s figures for nuclear output to determine nuclear’s output profile in the model.
• Biogas (e.g. anaerobic digestion, sewage gas and landfill gas) also tends to run relatively flat, not because it also couldn’t be varied (storage for a few hours of gas would not be too expensive or technically complex), but because of the incentives created by the subsidy regimes make it uneconomic to do anything other than export as the power is produced. We therefore use Elexon’s figures for this technology in the same way as for nuclear.

To date, it is so rare for the output of inflexibles to exceed total demand that there is not a great issue of contention. But it has started to occur, and increasing capacity of some of these technologies means that it is likely to become a significant issue. The model therefore needs a method to decide how the output of inflexibles will vary where there is insufficient demand. Our merit order, based on the economics and engineering issues of de-rating and up-rating the technologies and the history of how this has been handled in the relatively rare cases to date is: nuclear, biogas, solar, onshore wind, offshore wind. This is another case where the assumption is highly imperfect (for instance, in reality, it will vary within technology depending whether the projects are embedded or grid-connected) but some method must be chosen, and no other seems superior.

• the proportion of the existing building stock that has been improved to modern standards with regard to loft, cavity-wall and solid-wall insulation, and glazing, with an indication of the current proportions that are considered easy or difficult to improve, and
• the number of new houses and flats that have been built and the standards to which they have been built.
• the number of existing buildings demolished can also be accommodated by reducing the total figures under the section for existing buildings. The model relies on the modeller to choose realistic figures for the combined number of existing, demolished and new-build buildings. An unrealistic modeller could skew outcomes by assuming that we shall all live five to a flat in future. But they will then have to explain how that is desirable and deliverable in a democracy.

We do not yet incorporate equivalent costs for the gas network. This is a significant omission that needs correcting.

• Capital cost: £4bn
• Fixed cost: £1.5bn p.a.
• Variable cost: £10/MWh

• The Weighted Average Cost of Capital: 8%
• The Cost of Carbon: £50/tCO2e

• The investment may not be justified by the carbon benefit, or
• The assumed price for carbon is incorrect if necessary investments are not justified by their notional carbon saving.

• If the market is short and some gas-fired generation is required, the price of electricity in that period is the price of gas-fired electricity, and as the market is short, the price of gas-fired electricity is its operating cost plus an apportionment of its fixed/capital costs. If gas’s annual load factor is depressed because of high inflexible capacity producing many periods when gas is not required, the cost of gas-fired electricity in the periods when it is required will increase as the fixed/capital costs are spread over fewer periods.
• If the output from inflexible generators exceeds demand, the market is long, and the price is determined by the marginal operating cost of the last technology in the merit order required to meet that demand (typically offshore wind). The marginal operating costs of wind and solar are considered to be very low, so the marginal price of electricity in a long market is typically in this model very low. These are favourable assumptions for the deployment of storage, but hopefully realistic (i.e. the world towards which we are being driven is one in which storage should be able to buy electricity cheaply and sell at a high price).

• The annual usage of fossil fuels and electricity are inputs with defaults based on current usage. They are allocated to hourly periods on the above basis.
• An important constraint is that the model recognises the significant differences in on-vehicle conversion efficiency between Internal Combustion Engines (ICE) and electric motors, and tries to ensure that an adjustment to one is balanced by an equivalent adjustment to the other, such that the total post-conversion energy is not altered by a change to one component, though that total can be adjusted by the modeller. For example, given that electric motors are assumed by default to be 3.4 times more efficient than ICE on average, if we increase electricity’s share of road transport by 1 TWh, we reduce the non-electric component by 3.4 TWh and the total by 2.4 TWh. These default efficiency assumptions can also be varied by the modeller. The default efficiency for electric vehicles may look relatively low to proponents of the technology, but this is intended to reflect not only the efficiency in motion, but also inefficiencies in the charging process. We believe this is more realistic than the utopian figures sometimes used for electric-vehicle efficiency, but the modeller can apply their own assumptions. We have also seen lower efficiencies used by electric-vehicle sceptics.
• Another important assumption in the model is that users have some but not unlimited ability to choose to charge their electric vehicles when other electricity demands are low and prices are then presumably also low, and conversely avoid charging during peak demand periods. In other words, we assume that electric vehicles will provide a significant degree of demand smoothing to help with balancing, but that this will be largely preset according to behavioural patterns and expectations, and not responsive to unexpected system pressures outside expected patterns.
• There is a lot of talk of using vehicle batteries for electricity-system demand responsiveness. It seems to us that, whereas this might be true on the crude basis described above, it is fanciful on a more directed, on-demand basis. For example, few people will choose not to charge their car overnight so that they are unable to go to work the next day, no matter how much the system might need them to. This would have to be imposed against their will, and would be political suicide for any government attempting to instigate the capability. It is not inconceivable in this world of overmighty bureaucracies and misanthropic advisers, but we choose to assume a more benign, if less exactly-managed, world.

• The minimum cost must be more than people are paying for their electricity, or they would not be using the electricity.
• Willingness to curtail demand will be marginal. We may find a few users willing to curtail at the minimum cost, but as the scale of curtailment grows, people’s willingness to pay not to be curtailed (i.e. to pay for power, which equates to the opportunity cost of curtailment) will increase.
• This applies both to the scale and the frequency, i.e. each extra GW of curtailment in each period will be more expensive than the previous, and also each time someone has to curtail, it will be a bit more expensive to them than the last. Consider a manufacturing business asked to limit its electricity usage for one hour in the year. At a price, the cost is probably not too significant (depending on circumstance). Now consider if that business is asked to curtail for a week. It would at least be difficult and could be enough to put them out of business. They might accept a reasonable offer for the first, but would want a very high offer for the second.

• The 1st period is 1 GWh x £200/MWh = £200,000
• The 2nd period is (1 GWh x £202/MWh) + (1 GWh x £220/MWh) = £422,000
• Total cost of demand shedding for the two periods: £622,000